torerc.blogg.se - Easy chi square calculator

Determination of the expected numbers for each observational class is crucial.There are points to note when testing your hypothesis and calculating Chi Square: Chi-square requires that only numerical values should be used and not percentiles and or ratio. It should be noted that to determine Chi Square, first you need to determine the number expected in each category and the number observed.

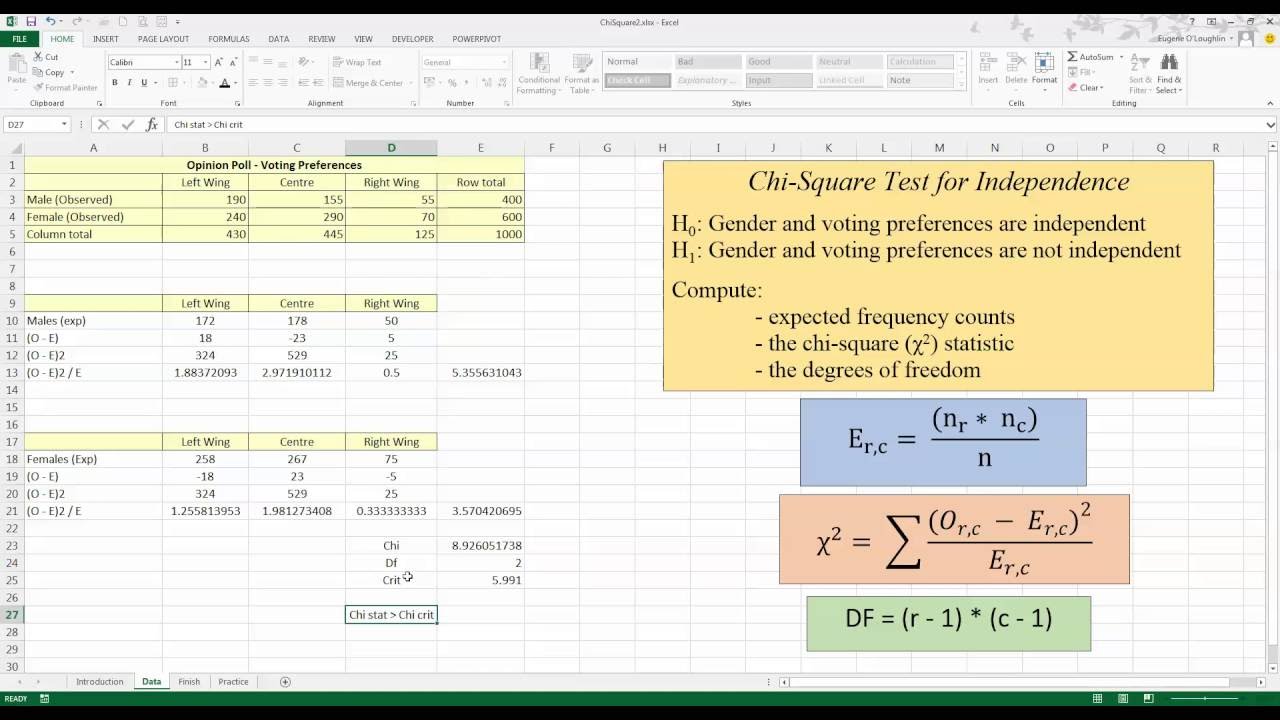
This means that the sum of the squared difference between the observed (O in the equation) data and the expected (E) over the expected data in all the possible categories. The expected value within each cell, if the null condition is true, is the product of the row and column total is divided by the overall sample for the test of independence and the sample divided by the number of levels of the single factor for the test of “goodness of fit.” The Chi-Square test of “goodness of fit” is then used to test the hypothesis that the total sample is distributed evenly among all levels of the relevant factor. The Chi-Square test of experiment is used to test for null hypothesis in that the frequencies (entered) within the cells is what is expected, given T. To conduct a Chi Square test, observed frequencies are entered, the sum of the elements within rows and columns (such as those in our calculator) are then computed (call this T).

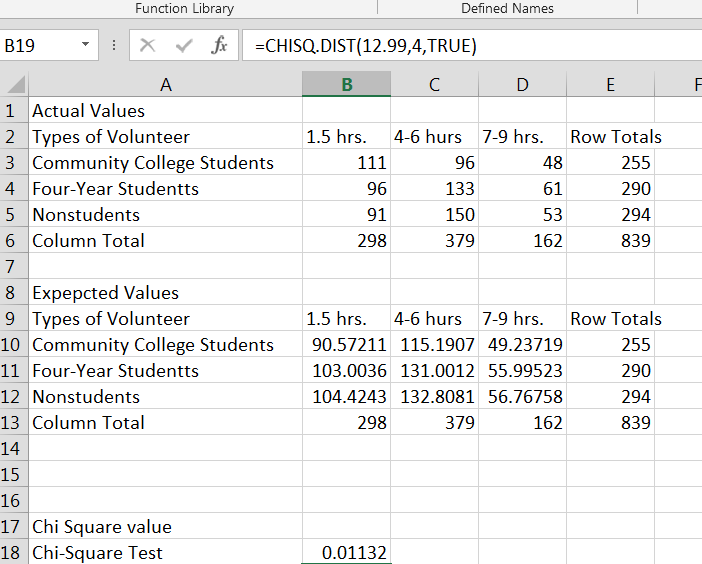
*The following information is not required to use our calculator, but is rather an in depth look at conducting a Chi Square Test by hand and the statistical process that comes with the resulting data. (This is also the formula that you would use if you needed to calculate statistical association by hand.)

It can also be used in analysis of nominal dataĬhi Square always tests for null hypothesis where there is no significant difference between the expected and observed results. The calculator above uses the following formula.

Chi Square is easy to calculate and interpret since you can get the correlating confirmation reports with ease.

It can be used in a wide variety of research contexts since it is not limiting in the data it accepts.

It can be applied in surveys, business, decision making, quality control, medical and biological control.

Chi Square accepts weaker, less accurate data as inputs thus having less status in the pantheon of the statistical tests.

Researchers should use it especially to see whether there are differences between two or more groups of participants.

Can be used with data that has been measured on a categorical scale.

While the Chi Square equation is complex, there are a number of reasons why it’s the preferred method of many data analysts: Why Top Researchers Use Chi Square for Data Analysis You can also find our Chi Square Calculator and an extended explanation of the process here.

It will tell you if your result is statistically significant or not. The table will output totals for the rows and columns, as well as the Chi-squared result.Fill in the group and category information.Ready to Calculate? Jump Right to the Calculator: It allows you to test out a number of hypothesizes with the aim of finding out if what you see is true, is really true, and for testing for the “goodness of fit” between the observed and expected data after several investigations. That’s where our Chi Square calculator comes in handy.Ĭhi Square is an especially powerful statistical method of assessing the goodness of fit (correlation) between observed values and the ones expected theoretically. Cross tabulation reports (called cross tabs) go a long way in helping to compare and analyze two questions and identify trends and patterns within your data… but determining statistical relevance is another matter.